参考：

先前的研究已经证明，拥有至少一个隐层的神经网络是一个通用的近似器，只要提高网络的深度，可以近似任何连续函数。因此，理想情况下，只要网络不过拟合，深度神经网络应该是越深越好。但是在实际情况中，在不断加神经网络的深度时，会出现一个 Degradation 的问题，即准确率会先上升然后达到饱和，再持续增加深度则会导致准确率下降。这并不是过拟合的问题，因为不光在测试集上误差增大，训练集本身误差也会增大。对此的解释为：当网络的层级很多时，随着前向传播的进行，输入数据的一些信息可能会被丢掉（激活函数、随机失活等），从而导致模型最后的表现能力很一般。

假设有一个比较浅的网络（Shallow Net）达到了饱和的准确率，那么后面再加上几个的全等映射层（Identity mapping），起码误差不会增加，即更深的网络不应该带来训练集上误差上升。而这里提到的使用全等映射直接将前一层输出传到后面的思想，就是 ResNet 的灵感来源。在ResNets中，作者通过shorcut connection操作，保证了网络的深度越深，模型的表现能力一定不会下降。

作者提出一个 Deep residual learning 框架来解决这种因为深度增加而导致性能下降问题。

假定某段神经网络的输入是 x，期望输出是 H(x)，即 H(x) 是期望的复杂潜在映射，但学习难度大；如果我们直接把输入 x 传到输出作为初始结果，通过下图“shortcut connections”，那么此时我们需要学习的目标就是 F(x)=H(x)-x，于是 ResNet 相当于将学习目标改变了，不再是学习一个完整的输出，而是最优解H(X) 和全等映射 x 的差值，即残差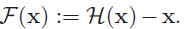

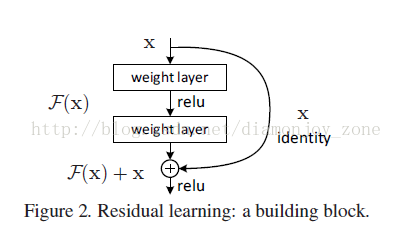
Shortcut 原意指捷径，在这里就表示越层连接，在 Highway Network 在设置了一条从 x 直接到 y 的通路，以 T(x, Wt) 作为 gate 来把握两者之间的权重；而 ResNet shortcut 没有权值，传递 x 后每个模块只学习残差F(x)，且网络稳定易于学习，作者同时证明了随着网络深度的增加，性能将逐渐变好。可以推测，当网络层数够深时，优化 Residual Function：F(x)=H(x)−x，易于优化一个复杂的非线性映射 H(x)。

在 ResNet 的论文中，除了提出残差学习单元的两层残差学习单元，还有三层的残差学习单元。两层的残差学习单元中包含两个相同输出通道数（因为残差等于目标输出减去输入，即，因此输入、输出维度需保持一致）的3´3卷积；而3层的残差网络则使用了 Network In Network 和 Inception Net 中的1´1卷积，并且是在中间3´3的卷积前后都使用了1´1卷积，先降维再升维的操作，降低计算复杂度。另外，如果有输入、输出维度不同的情况，我们可以对 x 做一个线性映射变换，再连接到后面的层。